SHA3をRustで実装した

Yuto Nakamura / 2023/05/05 (2039 Words, 12 Minutes)

Crypt Rust

SHA3をRustで実装しました。といっても、SHA3が実装したくて実装したわけではなく、Crystals-Kyberと呼ばれる最新の暗号方式を実装するために、SHA3を実装する必要があったので実装したまでです。今回実装した、SHA3の実装は、このリポジトリに含まれています。具体的にはsrc/sha3.rsにほとんどの実装があります。

https://github.com/yutyan0119/Kyber-rs

SHA3

Keccak（ケチャックと読むらしい）というハッシュ関数を用いた新しいハッシュ方式。SHA1, SHA2とは異なるアルゴリズムを採用しています。Keccakはあくまでもハッシュ化のアルゴリズムで、SHA3そのものとは異なる点に注意が必要です。SHA3はKeccakの一部パラメータを固定し、パディングの方法などを変更しています。NISTによって、標準化された次世代のハッシュ方式や！って感じがします。1 SHA1への攻撃が確立して同じアルゴリズムのSHA2もやばいんちゃうかとなって策定したが、SHA2は今のところ有効（多分ここで言う有効は現実的な時間で収まる）な攻撃手法がなく、まだ使えるらしい。じゃあSHA3を使うメリットってなんやって感じもしますが、こっちはこっちで出力長を可変にするSHAKEが標準化されてたりするからそういう部分も含めてええんやろうと思うことにしている。

Keccak

KeccakはSHA3の中で使われるハッシュ化アルゴリズム。ハッシュ化とは要するに、任意の長さのデータを取得して、それを内部でビット状態をある一定の操作を施してぐちゃぐちゃにして元のデータがわからないくらいまでぐちゃぐちゃにするということ。一定の操作なので、同じデータに対しては同じ出力が得られなければならない一方で、元に戻せたら怒られるという難しさがあります。

SHA3におけるKeccakのアルゴリズムをすごく簡単に言うと、以下のような感じ。

  1. データを一定量取得する。以下の操作はデータが取得できなくなるまで繰り返す。
  2. データに対して、決まった操作を24回する。
    • θ過程、ρ過程、π過程、χ過程、ι過程の順に操作を行う。それぞれの操作については後述
  3. データを取得できなくなったり、一定量に足らなくなったら、最後にパディングを行う。（これはすなわちちょうど一定量取って終わるようなときにもパディングを行うということ）
  4. もう一回決まった操作を24回する。
  5. 欲しい分だけデータを取得する。（ただし、SHAKEと呼ばれる任意の長さを取得するタイプのものでは、1回でデータが取り切れないこともあるので、取得 -> 24回ぐちゃぐちゃ -> 取得を繰り返すことがある）

これだけです。簡単に見えるし、実際ただこれを実装するだけならそんなに難しくない…多分。

データを取得する過程を吸収過程(absorb)と呼び、データを取得する過程をスクイーズ過程(squeeze)と呼びます。これは、Keccak少しずつデータを貯めながら内部でぐちゃぐちゃにし、それを最後に絞り出す構造をスポンジ構造と呼ぶところから来ているらしいです。

以下にスポンジ構造の図を示します。

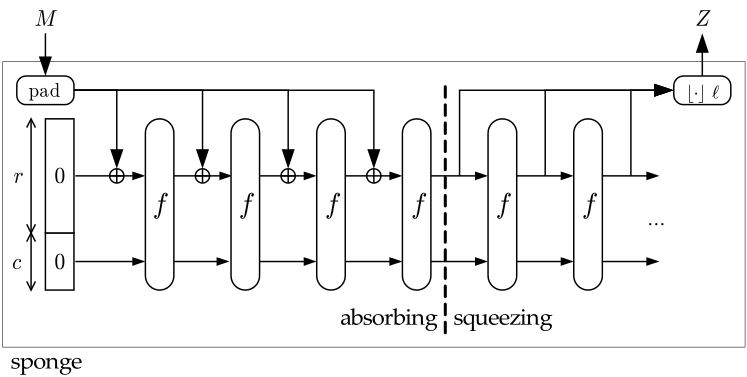
スポンジ構造の図

入力はMで表されていて、パディングされた後に、一定量ずつ入れられていることがわかります。rが入力を受け付けるブロックでcはcapacity blockと言われ、入出力には関わらりません。この部分は各操作時に一緒に操作される場所で、この部分のデカさがセキュリティに関わっているらしい。このr+cの部分をKeccakのstateと呼びます。入力はstateのrの部分とXORすることで入力されます。$f$ と書いてあるのは上に示した操作の部分です。

SHA3では、stateは一律で1600bitです。また、cの容量はSHA3-xxxのxxxの2倍と決められています。例えば、SHA3-512であれば、以下のようになります。

\[\begin{aligned} c &= 2 \times 512 = 1024 \\ r &= 1600 - 1024 = 576 \end{aligned}\]

このrのことを、rateと言います。後で入力を処理するときに出てきます。

$f$は、Keccakの公式サイト2の中で以下のような擬似コードで示されています。各配列のindexはmod 5であることに注意が必要です。（例えばx-1と書かれているところで、x = 0を代入すると実際の値は4になる。）

Keccak-f[b](A) {
  for i in 0..n-1
    A = Round[b](A, RC[i])
  return A
}

Round[b](A,RC) {
  # θ step
  C[x] = A[x,0] xor A[x,1] xor A[x,2] xor A[x,3] xor A[x,4],   for x in 0..4
  D[x] = C[x-1] xor rot(C[x+1],1),                             for x in 0..4
  A[x,y] = A[x,y] xor D[x],                           for (x,y) in (0..4,0..4)

  # ρ and π steps
  B[y,2*x+3*y] = rot(A[x,y], r[x,y]),                 for (x,y) in (0..4,0..4)

  # χ step
  A[x,y] = B[x,y] xor ((not B[x+1,y]) and B[x+2,y]),  for (x,y) in (0..4,0..4)

  # ι step
  A[0,0] = A[0,0] xor RC

  return A
}

r[x,y]とRCは以下のようにして表されます。

const r: [[usize; 5]; 5] = [
    [0, 36, 3, 41, 18],
    [1, 44, 10, 45, 2],
    [62, 6, 43, 15, 61],
    [28, 55, 25, 21, 56],
    [27, 20, 39, 8, 14],
];

const RC: [u64; 24] = [
    0x0000000000000001, 0x0000000000008082, 0x800000000000808a,
    0x8000000080008000, 0x000000000000808b, 0x0000000080000001,
    0x8000000080008081, 0x8000000000008009, 0x000000000000008a,
    0x0000000000000088, 0x0000000080008009, 0x000000008000000a,
    0x000000008000808b, 0x800000000000008b, 0x8000000000008089,
    0x8000000000008003, 0x8000000000008002, 0x8000000000000080,
    0x000000000000800a, 0x800000008000000a, 0x8000000080008081,
    0x8000000000008080, 0x0000000080000001, 0x8000000080008008,
];

また、擬似コードの中で表されているrotは、bitを左回転する操作です。例えば、b'10010'を左に2回転するとb'00101'を経てb'01010'になります。

fn rotl64(x: u64, n: usize) -> u64 {
  if n == 0 {x} else {(x << n | (x >> (64 - n)))}
}

このrotはspecification通りに実装すると、右回転になるのですが、後述する入力に関わる処理の都合上、左回転になります。

これでこの関数$f$の実装は後はやるだけ状態になります。今考えると、最初から道標を知っていれば、思ったより簡単。

以下に実際に実装したコードを示します。このコードの中で、stateは擬似コードにおけるAですが、1次元配列であり、state[x + 5 * y]でA[x,y]にアクセスできます。

fn theta(state: &mut [u64]) {
    let mut c: [u64; 5] = [0; 5];
    let mut d: [u64; 5] = [0; 5];
    for x in 0..5 {
        c[x] = state[x] ^ state[x + 5] ^ state[x + 10] ^ state[x + 15] ^ state[x + 20];
    }
    for x in 0..5 {
        d[x] = c[(x + 4) % 5] ^ rotl64(c[(x + 1) % 5], 1);
    }
    for x in 0..5 {
        for y in 0..5 {
            state[x + 5 * y] ^= d[x];
        }
    }
}

fn rho(state: &mut [u64]) {
    let mut current: [u64; 25] = state.try_into().unwrap();
    for x in 0..5 {
        for y in 0..5 {
            current[x + 5 * y] = rotl64(state[x + 5 * y], ROT[x][y]);
        }
    }
    state.copy_from_slice(&current);
}

fn pi(state: &mut [u64]) {
    let mut current: [u64; 25] = state.try_into().unwrap();
    for x in 0..5 {
        for y in 0..5 {
            current[x + 5 * y] = state[(x + 3 * y) % 5 + 5 * x];
        }
    }
    state.copy_from_slice(&current);
}

fn chi(state: &mut [u64]) {
    let mut current: [u64; 25] = state.try_into().unwrap();
    for x in 0..5 {
        for y in 0..5 {
            current[x + 5 * y] =
                state[x + 5 * y] ^ ((!state[(x + 1) % 5 + 5 * y]) & state[(x + 2) % 5 + 5 * y]);
        }
    }
    state.copy_from_slice(&current);
}

入出力の方法

あとは入出力を適当に処理してあげればOKです。まず、入出力の流れを擬似コードで示します。入力の流れはさっきも示しましたが、今度は擬似コードで示してみます。

while input.len >= rate {
  state ^= input[0..rate]
  f(state)
  input = input[rate..]
}
input = pad(input)
state ^= input

ここで、fはさっきの$f$です。また、rateとは、SHA3-xxxのxxxによって異なる一度に受け入れる入力bit数のことです。padはパディングを行う関数です。

1つポイントなのは、while文の条件がinput.len >= rate なことです。つまり、入力がちょうど受け入れられるbit数と等しくても、fを一回実行してから空のデータに対してパディングを行います。これを行うことで、偶然パディングいらずだったデータと、パディングが必要だったデータが同じ出力になることを防ぐことができます。パディングは簡単で、SHA3-xxxのときは、終端にSHA3であることを示す（可変長出力のSHAKEでないことを示す）ためにb'01'を足してから、その後にb'10.....01'とするだけです。これらを足し合わせて、SHA3ではinputの後にb'0110.....01'を足しています。

では、実際の僕のコードを見てみましょう。

pub fn keccak_absorb_once(state: &mut [u64], rate: usize, input: &[u8], mut len: usize, pad: u8) {
    //state initialization
    for i in state.iter_mut() {
        *i = 0;
    }

    let mut idx: usize = 0;
    //長いメッセージをrate byteずつ吸収する
    while len >= rate {
        //64bit = 8byteずつ吸収する
        for i in 0..rate / 8 {
            //inputをlittle endian 64bitとしてstateにxorする
            state[i] ^= u64::from_le_bytes(input[idx..idx + 8].try_into().unwrap());
            idx += 8;
        }
        len -= rate;
        //状態を更新する
        keccak_f1600(state);
    }
    //残ったメッセージを吸収する
    for i in 0..len {
        state[i / 8] ^= (input[idx + i] as u64) << (8 * (i % 8));
    }
    //先頭にpadをつける
    state[len / 8] ^= (pad as u64) << (8 * (len % 8));
    //最後のブロックに対してパディングを行う
    state[rate / 8 - 1] ^= 1u64 << 63;
}

ここで、入力にあるpadとは、SHAだったら0x06、SHAKEだったら0x1fです。これはさっき言ったpadding部分'b0110...01を思い出してくれればわかると思います。 それはそうとして、

    //先頭にpadをつける
    state[len / 8] ^= (pad as u64) << (8 * (len % 8));
    //最後のブロックに対してパディングを行う
    state[rate / 8 - 1] ^= 1u64 << 63;

が、意味わからんわとなると思います。少しずつ整理していきましょう。

実は、KeccakとSHA3では、ビット順（≠バイト順）が異なります。驚くべきことですが、SHA-3ではMSBファーストで、KeccakではLSBファーストみたいです。これはNICTがなんかしらんけどそうしたみたいです。3

つまりどういうことかというと、例えば、b'1001_1100'というデータがあったらKeccakの中では、'b0011_1100'に並べ直さないといけないということです。このとき、byte順は入れ替わりません。つまり、b'1001_1100_1010_0011'はb'0011_1001_1100_0101'になるということです。で、このあとにパディングが入る…。

しかし、実際にはbyteごとにbitの順番を反転させるなんて操作をやっていたら日が暮れます。そこでどうするかというと、paddingを込みでリトルエンディアンで読み込ませるという手法です。4

今、1byteの入力を受け取り、SHA3-256だとすると、最後の操作はこのようになります。

//メッセーじの吸収をリトルエンディアンで行う
state[0] ^= input[0] as u64 << (8 * 0);
//パディング開始埋め込み
state[0] ^= (pad as u64) << (8 * 1);
//パディング終了埋め込み
state[16] ^= 1u64 << 63;

このことからわかるのはパディングが必ず、最後に吸収されたメッセージの1つ上のbyteから始まっているということです。また、パディングの終わりは必ず、最後の64byteのMSBに示されていることがわかります。

//パディングしたあとのstate[0]はこんな感じ
b'00000000_00000000_00000000_00000000_00000000_00000000_00000110_00010110'
//パディングしたあとのstate[16]はこんな感じ
b'10000000_00000000_00000000_00000000_00000000_00000000_00000000_00000000'

確かにこれでパディングの開始も、終わりもリトルエンディアンで読み込まれていることがわかります。で、この後の操作で必要になる、XORやAND、NOTの操作はビット順に影響を受けないため、θ過程や、ρ過程のビット回転の操作だけ、反対にすれば問題ないらしいです。実際これでうまくいくのですが、なんやこれ。

こう考えれば良い

リトルエンディアンで読み込んだことで、嬉しいことがあります。それは、LSBファーストの効果が得られるということです。つまりこういうことです。

//MSB
b'00110011_11001100_10101010_01010101_00000000_00000000_00000000_00000000'

//LSB
b'11001100_00110011_01010101_10101010_00000000_00000000_00000000_00000000'

//little endianで読み込むMSB
b'00000000_00000000_00000000_00000000_01010101_10101010_11001100_00110011'

little endianを後ろから見てあげるとLSBファーストになってるやん！だからこれに操作してあげて（ただし回転だけ逆方向にしてあげる）最後に出力してあげれば同じやん！となってみんなハッピーですね。そう、回転を逆方向にするというのは、右からLSBが並んでるみたいな状態になってるからだったのです。なぁーんだ。

出力は簡単で、stateから必要な長さだけ取り出せばいいだけです。ただし、出力は[u8; 32]などに対して、stateは[u64; 25]なので、変換して取り出します。これもリトルエンディアンで良いです。じゃあもう一回上のを見てみましょう。今出力としてlittle endianで読み込むMSBの型のデータが得られます。本来であればLSBの形で出てきているので、これを各byteに関してbit順を反転して取り出し、MSBのやつが得たいものとなります。そこで、以下のようにして取り出すと、しっかり下からMSBになるように取り出せていることがおわかりいただけるかと思います。

pub fn sha3_256(out: &mut [u8; 32], input: &[u8], len: usize) {
    let mut state: [u64; 25] = [0; 25]; //state 1600 bits
    keccak_absorb_once(&mut state, SHA_256_RATE, input, len, 0x06);
    keccak_f1600(&mut state);
    for i in 0..32 {
        out[i] = (state[i / 8] >> (8 * (i % 8))) as u8;
    }
}

まとめ

SHA3のSpecificationや、Keccakチームの擬似コードを見ながら、RustでSHA3を実装しました。内部の状態遷移こそ簡単ですが、入出力周りがあまりにも複雑になっているので、正直嫌いです。LSBだかMSBだか知らないが統一して欲しいし、リファレンス実装が、Specificationと完全に合致しない方法で実装しているのもそれはどうなの？という気持ちになります。

NICTはこのSHA3の策定にあたって色々他にもトラブったみたいですが、（Wikipedia参照してください）せめてアルゴリズムに関してはもう少しまともにしろと思いました。この時期のNICTになんかあったんですかね、しらんけど。

でも実際MSBだがLSBだかどっちでも、内部のぐちゃぐちゃにする部分は変わらないので、僕はそれが良いと思っているんですが、なんでこうも複雑にしたんでしょうか。KeccakチームがNICT標準に合わせるのがだるかったのかもしれませんが…。

最後に、この記事の中で2度引用した筆者の記事3より、こんな言葉を引用して終わりにしたいと思います。

Let me tell you: FIPS 202’s explanation makes no sense.

教えてあげよう：FIPS 202（SHA3の仕様書）の説明は意味不明だ。

  1. https://csrc.nist.gov/publications/detail/fips/202/final ↩

  2. https://keccak.team/keccak_specs_summary.html ↩

  3. https://www.cryptologie.net/article/386/sha3-3-keccak-and-disturbing-implementation-stories/すべての混乱はこいつのせいだと書かれている。TSL1.3のようなプロセスを踏むべきで、SHA3は実質的にレファレンス実装を見なければ、誰も理解できないと言っている。 ↩ ↩2

  4. https://cryptologie.net/article/387/byte-ordering-and-bit-numbering-in-keccak-and-sha-3/ここで紹介されている手法で、レファレンス実装も大体の実装もこの方法でやっていると記述されている。 ↩

© 2023 Yuto Nakamura   •  Theme  Moonwalk